강화학습 정리 - Dynamic Programming
28 Feb 2019 | 강화학습 RL4. Dynamic Programming
Dynamic programing (DP) 은 알고리즘 범주 중 하나로, MDP 에서 완벽한 environment 의 model 이 주어졌을 때 optimal policy 를 계산할 수 있다. DP 는 reinforcement learning 에서 위의 조건을 만족하지 못하는 경우가 많기 때문에 사용에는 한계가 있지만, 여전히 이론적으로 매우 중요하다. DP 는 앞으로 다룰 내용들을 이해하는데 꼭 필요한 기반이 된다.
이 챕터에서는 주로 environment 가 finite MDP 라고 가정할 것이다. 또한 dynamics 가 $p(s^\prime,r \mid s,a)$ 으로 주어진다. $s \in \mathscr{S}, a \in \mathscr{A}(s), r \in \mathscr{R}, s^\prime \in \mathscr{S}^+$ ($\mathscr{S}^+$ 는 episodic 문제에서 terminal state 를 포함)
Reinforcement learning 과 DP 의 핵심 아이디어는 좋은 policy 를 찾기 위해서 value function 을 잘 구조화하는 것이다. 이 챕터에서는 DP 가 value function 을 계산하기 위해서 어떻게 사용하는지 알아볼 것이다. 만약 우리가 Bellman optimality equation 을 만족하는 $v_*$ 혹은 $q_*$ 를 알고 있으면 optimal policy 는 쉽게 구할 수 있다.
\[\begin{align*} v_*(s) &= \underset{a}{\text{max}} \mathbb{E} \left[ R_{t+1} + \gamma v_*(S_{t+1}) \mid S_t = s, A_t = a \right] \\ &= \underset{a}{\text{max}} \sum_{s^\prime, r}p(s^\prime, r \mid s, a) \left[ r + \gamma v_*(s^\prime) \right] \tag{4.1} \end{align*}\] \[\begin{align*} q_*(s,a) &= \mathbb{E} \left[ R_{t+1} + \gamma \underset{a^\prime}{\text{max}}q_*(S_{t+1}, a^\prime) \mid S_t=s, A_t = a \right] \\ &= \sum_{s^\prime, r}p(s^\prime, r \mid s, a) \left[ r + \gamma \underset{a^\prime}{\text{max}}q_*(s^\prime, a^\prime)) \right] \tag{4.2} \end{align*}\]앞으로 다루겠지만, DP 알고리즘은 Bellman equation 을 value function 의 근사치를 얻기 위한 업데이트 규칙으로 변환됨으로써 얻어진다.
Policy Evaluation (Prediction)
DP 에서 policy $\pi$ 에 대한 state-value function 을 policy evaluation 이라고 한다. 이전 장에서 모든 State s 에 대해 아래와 같이 정의 했었다.
\[\begin{align*} v_\pi(s) &\doteq \mathbb{E}_\pi\left[G_t \mid S_t=s \right] \\ &= \mathbb{E}_\pi \left[R_{t+1} + \gamma G_{t+1} \mid S_t=s \right] \tag{from (3.9)}\\ &= \mathbb{E}_\pi \left[R_{t+1} + \gamma v_{\pi}(S_{t+1}) \mid S_t=s \right] \tag{4.3}\\ &= \sum_a \pi(a \mid s) \sum_{s^\prime, r} p(s^\prime,r \mid s,a) \left[ r + \gamma v_\pi(s^\prime) \right], \text{for all } s \in \mathscr{S} \tag{4.4} \end{align*}\]$\pi(a \mid s)$ 는 policy $\pi$ 를 따랐을 때 state $s$ 에서 action $a$ 를 선택할 확률이다. 기댓값 $\mathbb{E}$ 에는 $\pi$ 에 따라 정해지기 때문에 $\pi$ 가 붙는다.
만약 environment 의 dynamic 를 완벽하게 알고 있다면, 식 (4.4) 는 선형 연립방정식으로 풀 수 있다. 그러나 우리가 해결하려는 문제에는 반복적인 계산으로 방법이 더 적합하다. 연속적인 approximate value function 을 $v_0, v_1, v_2 …, $ 으로 간주했을 떄, $v_\pi$ 에 대한 Bellman equation 을 사용해서 순차적으로 값을 계산할 수 있다. 여기서 각 $v_k$ 는 final state 를 포함한 모든 State $\mathscr{S}^+$ 에 맵핑 된다.
\[\begin{align*} v_{k+1}(s) &\doteq \mathbb{E}_\pi \left[R_{t+1} + \gamma v_k(S_{t+1}) \mid S_t=s \right] \\ &= \sum_a \pi(a \mid s) \sum_{s^\prime, r} p(s^\prime,r \mid s,a) \left[ r + \gamma v_k(s^\prime) \right], \text{for all } s \in \mathscr{S}, \tag{4.5} \end{align*}\]시퀀스 {$v_k$} 는 $k$ 가 무한으로 갈 때 $v_\pi$ 로 수렴한다. 이렇게 반복적으로 업데이트 하는 알고리즘을 iterative policy evaluation 이라고 한다.
$v_k$ 으로부터 $v_{k+1}$ 에 대한 근사값(approximation) 을 구하기 위해서, 각 state $s$ 에서 동일한 iterative policy evaluation 을 적용한다. 이 작업은 기존 $s$ 의 값을 새로운 값으로 대체하는데, 이 값은 기존 $s$ 에 이어지는 다음 state 들의 값과 expected immediate reward 로부터 계산된다. 이런 업데이트를 expected update 라고 한다. 각 iterative policy evaludation 는 새로운 appoximate value function $v_{k+1}$ 를 구하기 위해서 한번 모든 state 의 값을 업데이트 한다. DP 알고리즘에서 완료된 update 를 expected update 라고 한다. 왜냐하면 다음 state 를 샘플링 하는 것이 아니라 가능한 모든 다음 state 를 기반으로 업데이트 하기때문이다.
식 (4.5) 을 기반으로 iterative policy evaluation 을 프로그래밍 하기 위해서는 두개의 배열이 필요하다. 하나는 이전 값을 보관하는 $v_k(s)$ 이고, 또 다른 하나는 새로운 값을 보관하는 $v_{k+1}(s)$ 이다. 물론 하나의 배열을 사용해서 이전 값을 새로운 값으로 덮어씌워도 된다. 만약 그렇게 하면 업데이트되는 순서에 따라서 이미 업데이트 된 값이 이전 값 대신에 사용될 수도 있지만, 그렇다 하더라도 $v_\pi$ 에 수렴하게 된다. 사실 이런 방법이 두개의 배열을 사용하는 것보다 더 빠르게 수렴한다. 왜냐하면 업데이트된 새로운 값을 바로 사용할 수 있기 때문이다. 이런 알고리즘을 in-place 알고리즘 이라고 하며, 앞으로 DP 에서는 주로 이 방법을 사용할 것이다.
다음은 Iterative policy evaluation 의 in-place 버전에 대한 슈도코드다.

Policy Improvement
value function 을 계산하는 이유 중 하나는 더 나은 policy 를 찾는 것이다. 우리가 deterministic policy 를 갖는 value function $v_\pi$ 를 계산했다고 가정해보자. 특정 state $s$ 에서 policy 를 변경해야 하는지 알고 싶을 것이다. 물론 $v_\pi(s)$ 로부터 현재의 policy 를 따르는 것이 얼마나 좋은지는 알고 있다. 그러나 새로운 policy 를 적용하는 것이 더 나은 것일까 아니면 유지하는 것이 더 나을까? 이 질문에 답하기 위한 방법 중 하나는 $s$ 에서 $a$ 를 선택해보는 것이다. 그리고 그 다음에는 기존의 policy $\pi$ 를 따르는 것이다. 식으로 나타내면 다음과 같다.
\[\begin{align*} q_\pi(s,a) &\doteq \mathbb{E}_\pi \left[R_{t+1} + \gamma v_\pi(S_{t+1}) \mid S_t=s, A_t=a \right] \tag{4.6}\\ &= \sum_{s^\prime, r} p(s^\prime, r \mid s, a) \left[ r + \gamma v_\pi(s^\prime) \right] \end{align*}\]기준은 $v_\pi(s)$ 보다 크거나 작은지이다. 만약 더 크다면 $s$ 에서 한 번 $a$ 를 선택하고 그 뒤로 $\pi$ 를 따르는 것이 항상 $\pi$ 를 따르는 것보다 더 나을 것이다. 그렇다면 $s$ 에서 항상 $a$ 를 선택하는 것이 더 낫다고 예상할 수 있고, 새로운 policy 가 전체적으로 더 나은 policy 가 될 것이다.
$\pi$ 과 $\pi^\prime$ 를 모든 $ s \in \mathscr{S} $ 에서 deterministic policy 쌍으로 생각하자.
\[q_{\pi}(s, \pi^\prime(s)) \ge v_\pi(s) \tag{4.7}\]위의 식이 만족하기 위해서는 $\pi^\prime$ 이 $\pi$ 보다 같거나 더 좋아야 한다. 즉, 모든 $ s \in \mathscr{S} $ 에서 같거나 더 좋은 expected return 을 얻어야 한다.
\[v_{\pi^\prime}(s) \ge v_\pi(s) \tag{4.8}\]새로운 greedy policy $\pi^\prime$ 는 아래와 같이 구할 수 있다.
\[\begin{align*} \pi^\prime &\doteq \underset{a}{argmax}Q_\pi(s,a) \\ &= \underset{a}{argmax} \mathbb{E} \left[ R_{t+1} + \gamma v_\pi(S_{t+1}) \mid S_t=s, A_t=a \right] \tag{4.9} \\ &= \underset{a}{argmax} \sum_{s^\prime, r} p(s^\prime, r \mid s, a) \left[ r + \gamma v_\pi(s^\prime) \right] \end{align*}\]Greedy policy 는 one step 을 내다보고 $v_\pi$ 을 고려해서 가장 좋은 action 을 선택한다. 기존 policy 의 value function 에 대해 greedy 한 방법을 사용해서 기존의 policy 를 개선하여 새로운 policy 를 만드는 프로세스를 policy improvment 라고 한다. 만약 새로운 policy $\pi^\prime$ 이 기존 policy $\pi$ 와 유사하여 $v_\pi = v_{\pi^\prime}$ 이라면 식 (4.9) 로 부터 다음 식이 성립된다.
\[\begin{align*} v_{\pi^\prime}(s) &= \underset{a}{max} \mathbb{E} \left[ R_{t+1} + \gamma v_{\pi^\prime}(S_{t+1}) \mid S_t=s, A_t=a \right] \\ &= \underset{a}{max} \sum_{s^\prime, r} p(s^\prime, r \mid s, a) \left[ r + \gamma v_{\pi^\prime}(s^\prime) \right] \end{align*}\]그런데 위 식은 $v_{\pi^\prime}$ 을 $v_*$ 으로, 그리고 $\pi$ 을 $\pi^\prime$ 으로 두면 식 (4.1) 과 같다. 즉 Policy improvment 는 기존 policy 가 opimal 인 경우를 제외하고는 더 나은 policy 를 제공한다.
이번 세션에서 지금까지는 deterministic policy 의 특별한 경우만 고려했다. 그러나 일반적인 경우에 policy $\pi(a \mid s)$ 는 확률적인 stochastic policy 이다. 여기서 더 자세히 다루지는 않지만 이 세션에 있는 아이디어들은 쉽게 stochastic policy 로 확장될 수 있다. stochastic case 인 경우에 오직 하나의 action 만 선택할 필요는 없다. 만약에 최대화하는 여러개의 action 이 있다면, 확률을 나눠서 새로운 policy 에 부여할 수 있다.
Policy Iteration
한 번 $v_\pi$ 를 사용해서 policy $\pi$ 에서 개선된 policy $\pi^\prime$ 를 구혔다면, 다시 $v_{\pi^\prime}$ 을 사용해서 policy $\pi^{\prime\prime}$ 을 구할 수 있다. 따라서 개선되는 policy 와 value function 의 시퀀스를 얻을 수 있다.
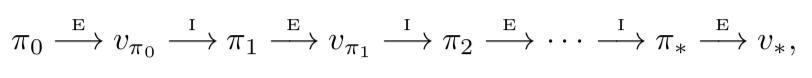
$\underset{\longrightarrow}{E}$ 는 policy evaluation 을 나타내고 $\underset{\longrightarrow}{I}$ 는 policy improvement 를 나타낸다. 각 policy 는 이전 policy 보다 개선됨을 보장한다. Finite MDP 는 유한(finite)개의 policy 가 존재하기 때문에, 이 프로세스는 유한(finite)번 iteration 에서 optimal policy 와 optimal value function 으로 수렴해야 한다. Optimal policy 를 찾는 이런 과정을 policy iteration 이라고 한다. 전체 알고리즘은 아래에 나와있다.

Value Iteration
Policy iteration 의 한가지 단점은 매 iteration 마다 policy evaluation 을 포함한다는 것이다. Policy evaluation 은 반복적으로 state set 을 여러번 sweep 하는 것을 필요로 하기 때문에, 그 자체적으로 시간이 쇼요되는 연산이다. 그렇다면 policy evaluation 에서 반복하는 작업을 줄일 수 없을까?
사실 policy iteration 이 수렴하는 것을 보장하면서 policy evaluation 과정을 줄일 수 있는 여러가지 방법이 있다. 그 중 중요한 한가지 방법은 오직 한 번만 sweep (각 state 를 한 번 업데이트) 하고 policy evaluation 을 끝내는 것이다. 이 알고리즘을 value iteration 이라고 한다. 이 알고리즘은 policy improvement 와 간략해진 policy evaluation 단계를 조합한 간단한 업데이트로 아래와 같이 작성할 수 있다.
\[\begin{align*} v_{k+1}(s) &= \underset{a}{max} \mathbb{E} \left[ R_{t+1} + \gamma v_{k}(S_{t+1}) \mid S_t=s, A_t=a \right] \\ &= \underset{a}{max} \sum_{s^\prime, r} p(s^\prime, r \mid s, a) \left[ r + \gamma v_k(s^\prime) \right], \text{for all } s \in \mathscr{S} \tag{4.10} \end{align*}\]Value iteration 을 이해할 수 있는 또 다른 방법으로는 Bellman optimality 식 (4.1) 을 참고하는 것이다. Value interation 은 간단하게 Bellman optimality 식을 업데이트 방식으로 변경함으로써 얻을 수 있다. 또한 모든 action 중에서 최댓값을 취하는 것을 제외하면 value iteration 업데이트 식이 policy evaluation 업데이트 식 (4.5) 와 같다. 이 둘의 관계를 더 자세하게 보기 위한 또 다른 방법은 이전 장에서 $v_\pi$ 와 $v_*$ 의 backup digram 을 비교하는 것이다. 아래는 value iteration 의 전체 알고리즘이다.

Value iteration 은 policy evaluation 의 one sweep 과 policy improvement 의 one sweep 을 효과적으로 조합한다. 각 policy impovement sweep 마다 policy evaluation sweep 을 여러번 해주는 것이 더 빠르게 수렴하기도 한다. 일반적으로 policy iteration 알고리즘은 policy evaluation 업데이트와 value iteration 업데이트로 이뤄진 sweep 의 시퀀스로써 생각할 수 있다. 왜냐하면 식 (4.10) 에 있는 max 연산만이 이 두개의 업데이트에서 차이점이기 때문이다. 단지 policy evaluation 의 sweep 중 일부에 max 가 추가된 것이다. 이 모든 알고리즘들은 discounted finite MDPs 에서 optimal policy 로 수렴한다.
Asynchronous Dynamic Programming
DP 의 유일한 단점은 MDP 의 모든 state set 을 연산한다는 것이다. 만약에 state set 이 매우 크다면 한 번 sweep 하는데 엄청나게 많은 비용이 든다. 예를 들어서 backgammon 게임에서는 $10^{20}$ 의 state 가 존재한다. 1초당 100만번 value iteration 을 할 수 있더라도 한 번 sweep 하는데 천년이 걸린다.
Asynchronous DP 알고리즘은 state set 의 체계적인(순서가 있는) sweep 으로 구성되어 있지 않은 DP 알고리즘이다. 이 알고리즘은 state 의 value 를 순서와 상관 없이 업데이트한다. 어떤 state 의 값은 다른 state 의 값들이 한 번 업데이트되기 전에 여러번 업데이트 되기도 한다. 그러나 정확하게 수렴하기 위해서는 asynchronous 알고리즘이 모든 state 값을 계속 업데이트해야 한다. 다시 말해서, 어떤 state 도 무시할 수 없다. Asynchronous DP 알고리즘은 업데이트 될 state 를 선택하는데 있어서 매우 큰 유연성을 제공한다.
이와 유사하게 비동기적으로 간략화된(asynchronous trucated) policy iteration 을 구현하기 위해서 policy evaluation 과 value iteration 업데이트를 조합할 수 있다. 여기서 더 자세하게 다루지는 않겠지만, 다양한 종류의 sweepless DP 에서 유연하게 사용할 수 있는 몇가지 다른 업데이트 방법들이 존재한다.
물론 sweep 을 피한다고 항상 더 적은 연산을 하지는 않는다. 단지 policy 를 더 향상시키기 위해서, 알고리즘이 말도 안되게 긴 시간을 사용할 필요는 없다는 것이다. 알고리즘의 진행 속도를 향상시키기 위해서 업데이트할 state 를 선택하는 유연함의 이점을 사용할 수 있다. 어떤 state 는 다른 state 들 처럼 자주 업데이트 될 필요가 없다. 먼약 optimal 을 찾는 것과 관련이 없는 state 가 있다면 업데이트를 건너 뛸 수 있다.
또한, 비동기(asynchronous) 알고리즘을 사용하면 실시간(real-time) 상호작용을 더 쉽게 조합하여 계산할 수 있다. MDP 문제를 풀기 위해서, agent 가 실제로 MDP 를 경험하는 시점에서 iterative DP 알고리즘을 사용할 수 있다. Agent 의 경험은 DP 알고리즘이 어떤 state 를 업데이트할지 결정한다. 동시에, DP 알고리즘으로 부터 얻은 마지막 value 와 policy 정보는 agent 의 의사결정(decision making)을 도와준다. 예를 들어서, agent 가 방문하는 state 를 업데이트 할 수 있다. 이렇게 하면 agent 와 가장 관련이 있는 state set 의 집합에 DP 알고리즘의 업데이트에 집중할 수 있다. 이런 방식은 reinforcement learning 에서 반복되는 주제다.
Generalized Policy Iteration
Policy iteration 은 현재 policy 에 맞게 value function 을 만드는 policy evaluation 과 현재 value function 에 맞게 greedy 한 policy 를 만드는 policy improvement 의 두 가지 프로세스로 이루어진다. Policy iteration 에서 이 두 가지 프로세스가 번갈아가면서 진행되고, 각 프로세스는 다른 프로세스가 시작하기전에 완료되지만 필수는 아니다. 예를 들어서, Value iteration 에서는 각 policy improvement 사이에 policy evaluation 가 딱 한 번씩 진행된다. 비동기(asynchronous) DP 에서는 더 미세하게 교차한다. 경우에 따라서 프로세스에서 오직 하나의 state 가 업데이트되어 다른 프로세스로 반환된다. 두 프로세스가 모든 state 를 업데이트 하기만 한다면, 궁극적으로 최종 결과는 optimal value function 과 optimal policy 로 수렴한다.
Policy evaluation 과 Policy improvement 의 세부사항과는 관계 없이 두 가지 프로세스가 상호작용하는 일반적인 아이디어를 generalized policy iteration (GPI) 로 표현한다. 거의 모든 reinforcement learning 은 GPI 로 설명된다. Policy 는 항상 value function 에 대해서 향상되고, value function 은 항상 policy 를 따르는 방향으로 나아간다. 만약 evaluation 프로세스와 improvement 프로세스가 안정화가 되고 결과가 바뀌지 않는다면, value function 과 policy 는 최적화(optimal)가 된 것이다. Value function 은 policy 에 대해서 일치할 때 안정화되고, policy 는 value function 에 대해서 greedy 하게 계산 되었을 때 안정화된다. 그러므로, 두 프로세스는 evaluation function(value function) 에 대해서 greedy 한 policy 를 찾은 경우에만 안정화된다. 이것은 Bellman optimality equation (4.1) 을 나타내고 있으며 policy 와 value function 이 optimal 하다는 것을 의미한다.
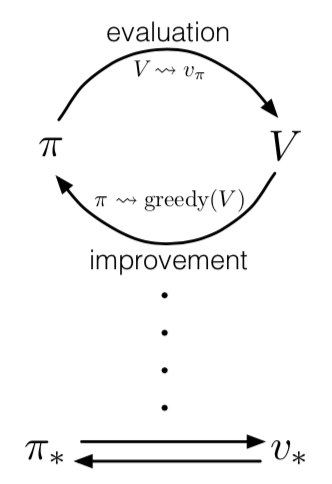
GPI 에서 evaluation 과 improvement 프로세스는 경쟁하면서 동시에 협력하는 것으로 볼 수 있다. 서로 반대 방향으로 당긴다는 의미에서 둘은 경쟁한다. 일반적으로, Value function 에 대해서 greedy 하게 policy 를 만드는 것은 변경되는 policy 에 대해서 value function 을 부정확하게 만든다. 그리고 policy 와 일치하는 방향으로 value function 을 만드는 것은 policy 가 더 이상 greedy 하지 않다는 것을 의미한다. 그러나 장기적인 관점에서, 이 두 프로세스는 optimal value function 과 optimal policy 이라는 공통된 솔루션을 찾기 위해서 상호작용한다.
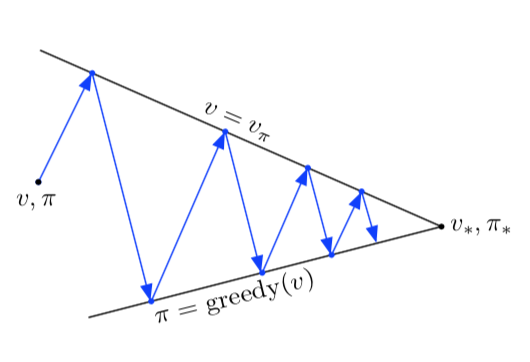
또한, GPI 에서 evaluation 과 improvement 프로세스의 상호작용을 두 경계나 목표(goal)측면에서 생각할 수도 있다. 예를 들어서, 아래 2차원 공간에서 두 선처럼 말이다. 사실 이것보다 더 복잡하지만, 다이어그램은 실제로 어떤일이 벌어지는지 보여준다.
Efficiency of Dynamic Programming
DP 는 매우 큰 문제에서는 실용적이지 않을 수 있다. 그러나 MDPs 를 해결하는 다른 방법들과 비교하면 상대적으로 DP 는 매우 효율적이다. 만약 기술적인 세부사항을 무시한다면, 최악의 경우 optimal policy 를 찾기 위한 시간은 state 와 action 수에 따른 다항식과 같다. $n$ 과 $k$ 를 state 와 action 의 개수라고 지칭하면, DP 식은 $n$ 과 $k$ 의 다항식보다 적은 계산을 한다는 것을 의미한다. DP 식은 policy 의 총 개수가 $k^n$ 일지라도, optimal policy 를 찾는 것을 보장한다. 이런 의미에서, DP 는 모든 policy 를 직접 조사하는 것(direct search) 보다 기하급수적으로 더 빠르다.
때때로, DP 는 차원의 저주(curse of dimentionality) 때문에 실용성에 한계가 있다고 여겨지기도 하는데, 이는 state 의 수가 state 변수의 수에 따라 기하급수적으로 증가하기 때문이다. 비록 큰 state 셋은 문제를 해결하는데 어려움을 야기하지만, 이는 문제 자체의 본질적인 어려움이지 솔루션으로서 DP 의 문제는 아니다. 실제로 DP 는 큰 state 공간에서 문제를 해결하는데 있어서, direct search 나 linear programming 보다 더 적합하다.
실제로 DP 는 수백만의 state 를 갖는 MDPs 문제를 해결하는데 사용되고 있으며 policy iteration 과 value iteration 도 널리 사용되고 있다. 사실 이런 방법들은 각각 가지고 있는 이론적으로 최악인 경우보다 훨씬 빠르게 수렴하며, 이는 특히 value function 이나 policy 의 초기화가 잘 된 경우 나타난다.
Summary
이번 챕터에서는 Finite MDPs 를 해결하는 것과 관련이 있는 dynamic programming 의 기본 아이디어와 알고리즘에 대해 알아보았다. Policy evaluation 은 주어진 policy 의 value function 을 반복적으로 계산하는 것을 나타낸다. 그리고 policy improvement 는 주어진 value function 을 고려해서 더 나은 policy 를 계산하는 것을 나타낸다. 이 두가지를 함께 사용해서 DP 에서 가장 유명한 policy iteration 과 value iteration 을 계산할 수 있다. 이들 중 한가지를 이용해서 MDP 에 대한 완벽한 정보가 주어진 finite MDPs 의 optimal policy 와 value function 을 계산할 수 있다.
Classical DP 는 state set 을 sweep 을 통해서 수행하며, 각 state 에 대해서 expected update 한다. State 하나의 업데이트는 가능한 모든 다음 state 의 값(value)과 각 state 가 발생할 수 있는 확률을 기반으로 수행된다. Expected update 는 Bellman equation 과 관련이 있다. 업데이트에서 더 이상 결과값이 변하지 않으면 Bellman equation 을 충족하는 값으로 수렴된 것이다. 4개의 주요한 값($v_\pi, v_*, q_\pi, q_*$) 에 대한 Bellman equation 과 그에 해당하는 expected update 가 있다. 또한 DP 업데이트를 직관적으로 볼 수 있는 backup diagram 이 있다.
사실 거의 모든 reinforcement learning 은 generaized policy iteration(GPI) 의 관점에서 볼 수 있다. GPI 는 appoximate policy 와 appoximate value function 을 중심으로 돌아가는 두 개의 상호작용 프로세스의 일반적인 아이디어다. 하나의 프로세스(policy evaluation)는 policy 를 주어진 것으로 여기고 value function 을 policy 에 대한 true value function 에 가깝도록 변경해간다. 또 다른 프로세스(policy imporvement)는 value function 을 주어진 것으로 여기고 value function 에 맞도록 policy 를 더 좋은 방향으로 변경해간다. 비록 각 프로세스가 다른 프로세스의 기준을 변경하더라도, 전반적으로 공통 솔루션을 찾기 위해서 함께 동작한다.
모든 것은 다음 state 값의 추정치(estimate)를 기반으로 state 값의 추정치(estimate)를 업데이트 한다. 즉 다른 추정치를 이용해서 추정치를 업데이트하는 것이다. 이런 아이디어를 bootstrapping 이라고 한다. 많은 reinforcement learning 에서는 bootstrapping 을 수행한다. 다음 챕터에서는 model 을 요구하지 않고, bootstrap 을 수행하지 않는 방법에 대해서 알아볼 것이다. 그리고 그 다음 챕터에서는 model 은 요구하지 않지만 bootstrap 을 수행하는 방법에 대해 알아볼 것이다.
Comments